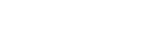Escutoides, o el día que los biólogos sorprendieron a los físicos

En todos lados hay jerarquías, justificadas o no. Hasta en las ciencias. Por eso los físicos tienden a sentirse superiores a los biólogos (y a los químicos), y los matemáticos a todos ellos.

Abundan los aspectos de la biología que son explicados y hasta predichos gracias a principios físicos (el grosor de las patas de elefantes y dinosaurios, digamos, comparado con las de los insectos) o matemáticos (por qué las conchas de los caracoles forman precisamente esas espirales y no otras).

Pero el 27 de julio de 2018 se publicaron los resultados de una investigación que descubrió, a partir de la biología, nada menos que una nueva forma geométrica, un sólido tridimensional nunca antes conocido, que resulta vital para entender el desarrollo de los seres vivos, y les da algo nuevo que estudiar a matemáticos y físicos.

En un simpático artículo en el diario El País Clara Grima, matemática de la Universidad de Sevilla y una de las investigadoras que participaron en el descubrimiento, cuenta con mucha gracia la historia.

Resulta que sus colegas Luis Manuel Escudero y Alberto Márquez, junto con ella misma, estaban tratando de explicar qué forma tienen las células que conforman uno de los tejidos más comunes en los animales, el epitelial. Los epitelios son los tejidos que recubren todas las superficies de nuestro cuerpo, incluyendo no sólo la piel sino las mucosas en la superficie de las cavidades del cuerpo (boca, intestino…) y nuestros órganos internos.

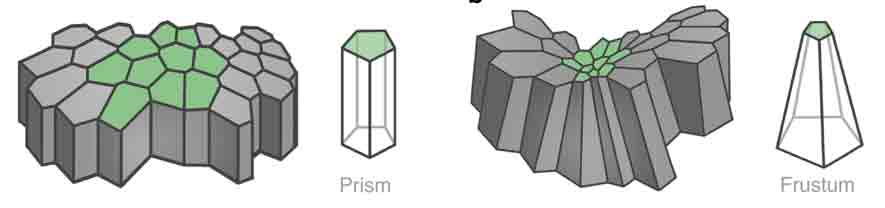
Imagen superior: el esquema clásico de libro de texto que muestra las células epiteliales como prismas y pirámides (Fuente: ‘Nature Communications’).

Células con una forma extraña

Los epitelios están formados por una o varias capas de células paralelas que están unidas estrechamente. Por ello, se suponía –y así aparece hoy en todos los libros de texto– que estas células tenían forma de prismas, en epitelios planos, o de pirámides truncadas, en epitelios curvos, con bases pentagonales o hexagonales. Algo semejante a los prismas basálticos que existen en San Miguel Regla, en el Estado de Hidalgo.

Pero tanto las observaciones como los modelos en computadora de los investigadores indicaban que si las células tuvieran estas formas sencillas, no podrían formar tejidos compactos y flexibles sin dejar espacios. Es más, sus modelos predecían que las células deberían tener una forma extraña, en la que la base de un prisma podía ser hexagonal por abajo y pentagonal por arriba.

Cuando examinaron con más cuidado sus tejidos (de glándulas salivales de mosca), descubrieron que, efectivamente, las células de los epitelios curvados adoptaban esa forma.

Imagen superior: el escutelo del escarabajo ‘Protaetia speciosa’.

Una solución geométrica

Intrigados, contactaron con matemáticos para preguntarles cómo se llamaba esa figura, y descubrieron que no tenía nombre. Así que, como homenaje a Escudero, decidieron llamarla «escutoide» (aunque luego justificaron el nombre aludiendo a que la forma recuerda al «scutum» –escudo– que aparece en la caparazón de ciertos escarabajos).

Al final en la investigación, publicada en la revista Nature Communications y titulada «Escutoides: una solución geométrica al empaquetamiento tridimensional de los epitelios», participaron 16 autores: además de los investigadores de la Universidad de Sevilla, incluyó a colegas ingleses y estadounidenses, entre los que había biólogos moleculares, matemáticos, físicos y especialistas en ingeniería biomolecular.

Entonces, ¿qué forma tiene un escutoide? Pues es un prisma o pirámide truncada una de cuyas bases es hexagonal y la otra pentagonal, por lo que obligadamente una de sus aristas tiene la forma de una letra Y. (Mucha gente dice que parecen unos saleros de diseñador… seguramente pronto habrá quien los saque a la venta.)

¿Por qué necesitan las células adoptar formas tan complejas? Es un asunto de biología, física y matemáticas. El cuerpo animal se desarrolla a partir de una sola célula, el óvulo fecundado, que se va multiplicando y luego forma capas que darán origen a los distintos tejidos y órganos del cuerpo.

Uno tiende a imaginar a las células como simples bolsitas más o menos esféricas llenas de citoplasma. En realidad, conforme las células de un epitelio crecen, van ocupando más espacio pero están limitadas por sus vecinas.

Por eso, el escutoide es la forma geométrica que les permite ocupar de manera más eficiente todo el espacio disponible sin dejar huecos –requisito indispensable para que el epitelio pueda cumplir su función de barrera– y al mismo tiempo poder formar tejidos curvos y flexibles (cosa que no sería posible sólo con prismas o pirámides truncadas, y menos con esferitas).

La forma que reduce al mínimo la superficie celular

En última instancia, se trata de un problema de física: el escutoide es la forma que reduce al mínimo la superficie celular y por tanto la energía que necesitan las células para formar el epitelio. (Algo similar sucede, por ejemplo, con las burbujas: la forma de mínima energía para una burbuja aislada es una esfera, pero muchas burbujas adheridas una con otra, como ocurre en la espuma, adoptarán formas tipo escutoide.)

El descubrimiento de los escutoides dista de ser sólo una curiosidad: su estudio permitirá entender mucho más detalladamente el desarrollo de los tejidos durante el crecimiento de los seres vivos, y quizá desarrollar métodos de análisis para detectar, por ejemplo, crecimientos anormales. Además, podría ser útil en la naciente tecnología de cultivo de tejidos y órganos. Y podría tener aplicaciones fuera de la biología, por ejemplo en la ingeniería y el diseño, para proyectar materiales, edificios o empaques más resistentes y eficientes. Y, en matemáticas, quizá para abrir nuevas líneas de investigación en geometría. Todo a partir de unos biólogos que querían entender cómo se agrupan las células del epitelio del glándula salival de una mosca.

Así que la próxima vez que alguien le hable de investigación interdisciplinaria, sólo recuerde a los escutoides de los que están hechos nuestros tejidos.

Imagen de la cabecera: un escarabajo con escutelo, la estructura parecida a un escutoide por el que esta forma geométrica recibió su nombre. | Wikimedia Commons.

Copyright del artículo © Martín Bonfil Olivera. Publicado previamente en La ciencia por gusto y editado en Cualia.es con permiso del autor. Reservados todos los derechos.